1. Bellman-Ford 알고리즘이란 무엇입니까?
- 노드에서 다른 모든 노드까지의 최단 거리를 찾는 알고리즘 + 음의 주기가 있는지 알기
- 다익스트라와 달리 음수 가중치와 함께 사용할 수도 있습니다.
- 시간 복잡도: O(NE) (N: 노드 수, E: 에지 수)
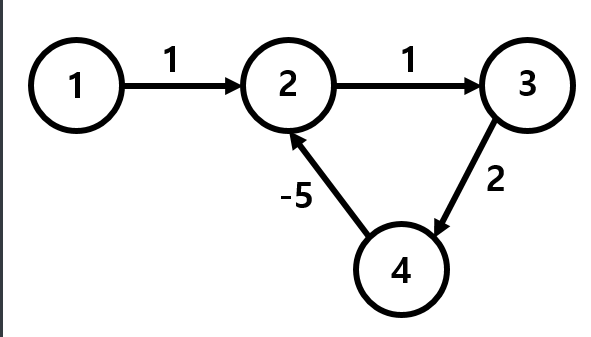
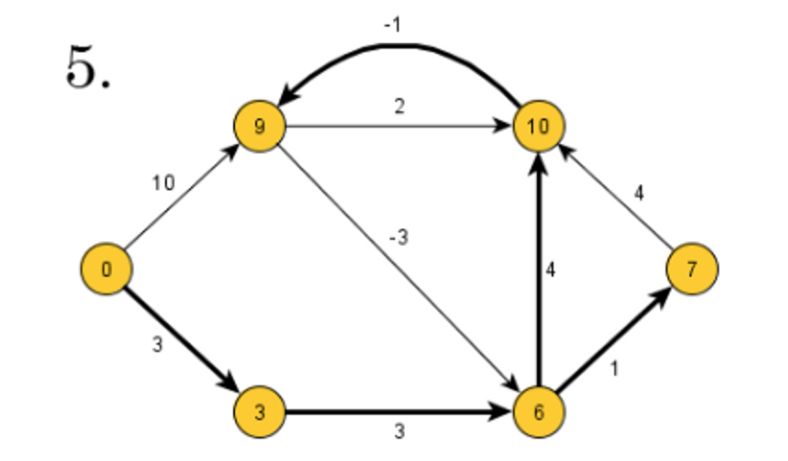
- 다음 다이어그램이 있다고 가정합니다.
- Dijkstra를 사용하여 노드 1에서 모든 노드까지의 거리 찾기
- 1 -> 2 = 1
- 1 -> 2 -> 3 = 2
- 1 -> 2 -> 3 -> 4 = 4
- 노드 2는 이미 방문한 적이 있으므로 경로 4 -> 2는 고려하지 않습니다.
- 따라서 1 -> 2의 최단 경로는 1입니다.
- 그러나 1 -> 2에서 실제 최단 경로는 -∞입니다.
- Bellman-Ford 알고리즘은 이 문제를 해결하기 위해 개발되었습니다.
2. 알고리즘 동작 원리
- 시작점을 선택하십시오.
- 모든 에지를 검색하므로 시작 노드에서 다른 노드까지의 거리가 INF가 아닌 경우 거리가 업데이트됩니다. 이 과정 (정점 수 -1)가능한 한 여러 번 계속
- 마지막 두 개를 수행하십시오.
2단계에서 (꼭지점 수 – 1)까지 계속하는 이유는 V 꼭지점과 E 모서리를 갖는 가중치 그래프에서 꼭지점 A에서 꼭지점 B까지의 최단 거리가 최대 V-1강아지의 끝을 통과하기 때문입니다.
V-1개 이상의 정점을 방문하면 결국 중복 방문이 발생하므로 최단 경로를 결정할 수 없습니다.
또한 3단계가 끝나면 2단계를 다시 수행하여 음의 주기가 있는지 판단한다. V 꼭지점을 통과한 후 최단 경로를 업데이트하면 비용이 무한대로 업데이트되기 때문에 음의 순환이 발생하고 최단 경로를 얻을 수 없습니다.
사진과 함께 알아봅시다.
1. 재설정
시작점(시작 노드)을 제외한 모든 노드까지의 최단 거리를 무한대로 초기화합니다. 시작점으로부터의 거리는 0입니다.
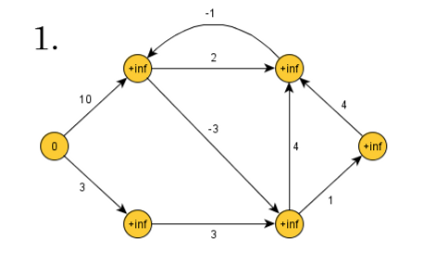
2. 최단거리 계산
V-1 동안 모든 모서리가 검사됩니다.
현재 에지까지의 최단 거리 + 현재 에지까지의 거리가 현재 에지의 target에 저장된 최단 거리보다 짧으면 최단 거리를 업데이트합니다.
for(i=1; i<V; i++) // V-1번
for(Edge now : EdgeList) // 모든 엣지에 대해
if(distance(now.end) > dist(now.start) + now.cost)
distance(now.end) = dist(now.start) + now.cost
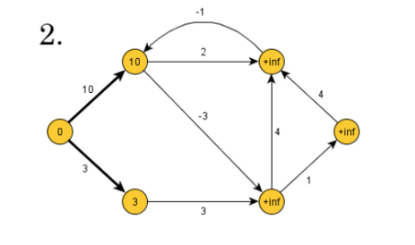
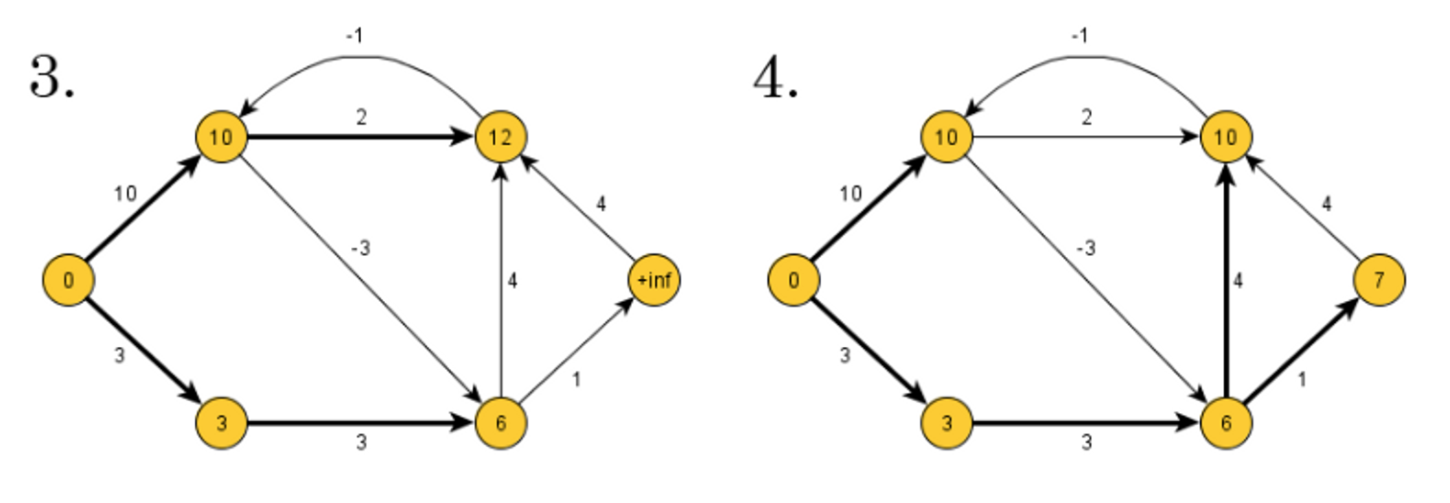
이 시점에서 에지의 시작점이 무한이면 업데이트가 되지 않으므로 첫 번째 검색에서는 시작 꼭지점에 연결된 에지만 업데이트 됩니다.
즉, 첫 번째 탐색에서 최대 하나의 모서리를 포함하는 최단 거리를 구합니다.
두 번째는 여전히 한 방향으로 갈 수 있으므로 최대 두 개의 가장자리를 포함하는 최단 거리를 얻습니다.
따라서 i번째 탐색에서는 i번째 edge를 포함하는 최단 거리를 구하게 되며, 경로에 어떠한 싸이클도 발생하지 않아야 하므로 최단 거리 탐색은 V-1로 끝난다.
3. V. 검색 – 확인 프로세스
최단 거리 탐색은 V-1에서 끝나므로 탐색을 계속해도 업데이트가 발생하지 않아야 합니다.
업데이트는 Vth에서 발생 → 음의 주기가 존재합니다.
for(Edge now : EdgeList)
if(distance(now.end) > dist(now.start) + now.cost)
return false // 음수 사이클 존재
return true예제 문제 해결
https://www.acmicpc.net/problem/11657
문제
N개의 도시가 있습니다. 그리고 한 도시에서 출발하여 다른 도시에 도착하는 M-버스가 있습니다. 각 버스는 A, B, C로 나타낼 수 있으며, 여기서 A는 출발 도시, B는 목적지 도시, C는 버스 운행 시간입니다. 시간 C가 양수가 아닌 경우가 있습니다. C = 0은 텔레포트를 의미하고, C < 0은 타임머신을 이용한 시간 여행을 의미합니다.
도시 1에서 다음 도시까지 가장 빠른 시간을 찾는 프로그램을 작성하십시오.
기입
도시의 수 N(1 ≤ N ≤ 500)과 버스 노선의 수 M(1 ≤ M ≤ 6,000)이 첫 번째 줄에 주어집니다. 두 번째 라인부터 M 라인에는 버스 노선 정보 A, B, C(1≤A, B≤N, -10,000≤C≤10,000)가 주어진다.
누르다
도시 1에서 시작하여 특정 도시까지 시간을 무한히 거꾸로 되돌릴 수 있으면 첫 번째 줄에 -1을 인쇄하십시오. 그렇지 않으면 1번 도시에서 2번 도시, 3번 도시, …, N번 도시로 가는 가장 빠른 시간이 N-1행에 걸쳐 각 행에 순차적으로 인쇄된다. 해당 도시로 가는 경로가 없으면 대신 -1을 반환합니다.
public class BOJ11657 {
static class Edge {
int start, end, cost;
public Edge(int start, int end, int cost) {
this.start = start;
this.end = end;
this.cost = cost;
}
}
static int N, M;
static long() dist;
static Edge() edgeList;
static int ans;
static boolean isUpdated;
static final int INF = 100000000;
public static void main(String() args) throws Exception {
/* INPUT */
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
edgeList = new Edge(M + 1);
int a, b, c;
for (int i = 1; i <= M; i++) {
st = new StringTokenizer(br.readLine());
a = Integer.parseInt(st.nextToken());
b = Integer.parseInt(st.nextToken());
c = Integer.parseInt(st.nextToken());
edgeList(i) = new Edge(a, b, c);
}
/* 1. 배열 초기화 */
dist = new long (N+1);
for (int i = 2; i <= N; i++) {
dist(i) = INF;
}
BellmanFord();
/* OUTPUT */
if (isUpdated) { // 음수 사이클이 발생한 경우
System.out.print(-1);
}
else {
StringBuilder sb = new StringBuilder();
for (int i = 2; i<=N; i++) {
if (dist(i)==INF) { // 가는 경로가 없는 경우
sb.append("-1\n");
}
else {
sb.append(dist(i)+"\n");
}
}
System.out.print(sb);
}
}
static void BellmanFord() {
/* 2. 최단거리 계산 */
for (int i = 1; i < N; i++) { // N-1번 탐색
for (Edge now : edgeList) { // 모든 엣지에 대해
if (dist(now.start) == INF) // 시작점이 무한대면 어차피 갱신이 안됨
continue;
dist(now.end) = Math.min(dist(now.end), dist(now.start) + now.cost); // 갱신
}
}
/* 3. 사이클 발생 여부 확인 */
for (Edge now : edgeList) {
if (dist(now.start) + now.cost < dist(now.end)) {
isUpdated = true;
return;
}
}
}
}
참조 페이지

